1、面面垂直

面面垂直的判定定理：一個平面過另一平面的垂線，則這兩個平面相互垂直。如果一個平面的垂線平行于另一個平面，那么這兩個平面互相垂直。如果兩個平面的垂線互相垂直，那么這兩個平面互相垂直。

面面垂直的判定定理

1、在一個平面內(nèi)做2條相交直線，另一個平面內(nèi)有一條直線垂直于這兩條相交直線，則面面垂直。

2、如果兩個平面互相垂直，那么在一個平面內(nèi)垂直于它們交線的直線垂直于另一個平面，則面面垂直。

3、如果一個平面經(jīng)過另一平面的垂線，則這兩個平面相互垂直。

面面垂直的證明方法

1、定義法：如果兩個平面所成的二面角為90deg;，那么這兩個平面垂直。

2、判定定理：如果一個平面經(jīng)過另一個平面的一條垂線，那么這兩個平面互相垂直。

3、如果一個平面內(nèi)任意點在另外一個平面的射影均在這兩個平面的交線上，那么垂直。

4、如果N個互相平行的平面有一個垂直于一個平面，那么其余平面均垂直這個平面。

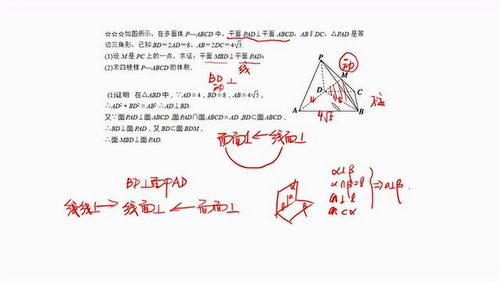
2、面面垂直的判定定理是什么？

共三個定理：

1、在一個平面內(nèi)做2條相交直線，另一個zhi平面內(nèi)有一條直線垂直于這兩條相交直線，則面面垂直。

2、如果兩個平面互相垂直，那么在一個平面內(nèi)垂直于它們交線的直線垂直于另一個平面。 面面垂直。

3、如果一個平面經(jīng)過另一平面的垂線,則這兩個平面相互垂直。

一個平面過另一平面的垂線，則這兩個平面相互垂直。

幾何描述：若a⊥β，a?α，則α⊥β

證明：任意兩個平面關系為相交或平行，設a⊥β，垂足為P，那么P∈β

∵a?α，P∈a

∴P∈α

即α和β有公共點P，因此α與β相交。

設α∩β=b，∵P是α和β的公共點

∴P∈b

過P在β內(nèi)作c⊥b

∵b?β，a⊥β

∴a⊥b，垂足為P

又c⊥b，垂足為P

∴∠aPc是二面角α-b-β的平面角

∵c?β

∴a⊥c，即∠aPc=90°

根據(jù)面面垂直的定義，α⊥β

3、面面垂直的判定方法

面面垂直的判定方法如下：

1、在一個平面內(nèi)做2條相交直線，另一個平面內(nèi)有一條直線垂直于這兩條相交直線，則面面垂直。

2、如果兩個平面互相垂直，那么在一個平面內(nèi)垂直于它們交線的直線垂直于另一個平面，則面面垂直。

3、如果一個平面經(jīng)過另一平面的垂線，則這兩個平面相互垂直。

面面垂直的證明方法：

1、利用直角三角形中兩銳角互余證明。

由直角三角形的定義與三角形的內(nèi)角和定理可知直角三角形的兩個銳角和等于90°，即直角三角形的兩個銳角互余。

2、勾股定理逆定理。

3、圓周角定理的推論。

直徑所對的圓周角是直角，一個三角形的一邊中線等于這邊的一半，則這個三角形是直角三角形。

4、三垂線定理。

在平面內(nèi)的一條直線，如果和穿過這個平面的一條斜線在這個平面內(nèi)的射影垂直，那么它也和這條斜線垂直。

立體幾何的平行關系與垂直關系的證明：

一、平行關系。

1、線線平行。

在同一平面內(nèi)無公共點的兩條直線平行；公理4（平行公理）；線面平行的性質。4.面面平行的性質；垂直于同一平面的兩條直線平行。

2、線面平行。

直線與平面無公共點；平面外的一條直線與平面內(nèi)的一條直線平行；兩平面平行，一個平面內(nèi)的任一直線與另一平面平行。

3、面面平行。

兩個平面無公共點；一個平面內(nèi)的兩條相交直線分別與另一平面平行。

二、垂直關系。

1、線線垂直。

直線所成角為90°；一條直線與一個平面垂直，那么這條直線與平面內(nèi)的任一直線垂直。

2、線面垂直。

一條直線與一個平面內(nèi)的任一直線垂直；一條直線與一個平面內(nèi)的兩條相交直線都垂直；面面垂直的性質；兩條平行直線中的一條垂直與一個平面，那么另一直線也與此平面垂直；一條直線垂直與兩個平行平面中的一個，那么這條直線也與另一平面垂直。

4、證明面面垂直四個方法

1。證明平面與平面垂直的方法：（1）利用定義：證明二面角的平面角為直角；（2）利用“面面垂直”判定定理：如果一個平面經(jīng)過另一個平面的一條垂線，則這兩個平面互相垂直。簡述為：“若線面垂直，則面面垂直”。

2.平面與平面垂直的性質：（1）兩個平面垂直的性質定理：如果兩個平面垂直，那么在一個平面內(nèi)垂直于它們交線的直線垂直于另一個平面。簡述為：“若面面垂直，則線面垂直”。

（2）如果兩個平面互相垂直，那么經(jīng)過第一個平面內(nèi)的一點垂直于第二個平面的直線，在第一個平面內(nèi)。此性質可以作為面面垂直的性質定理直接應用

3．“面面垂直”的判定定理和性質定理和“線面垂直”的判定定理和性質定理有密切聯(lián)系，若注意到這一聯(lián)系，則既可加深對垂直關系概念的系統(tǒng)理解，

又可加強對有垂直關系的有關定理之間的內(nèi)在聯(lián)系的認識。例題：如圖，過s引三條長度相等但不共面的線段sa、sb、sc，且∠asb=∠asc=60°，∠bsc=90°。求證：平面abc⊥平面bsc。作ad⊥平面bsc，d為垂足。

請?zhí)砑游⑿盘栕稍儯?9071507959

在線報名

上一篇：面試部長自我介紹,學生會部門面試自我介紹怎么寫

下一篇：暫無