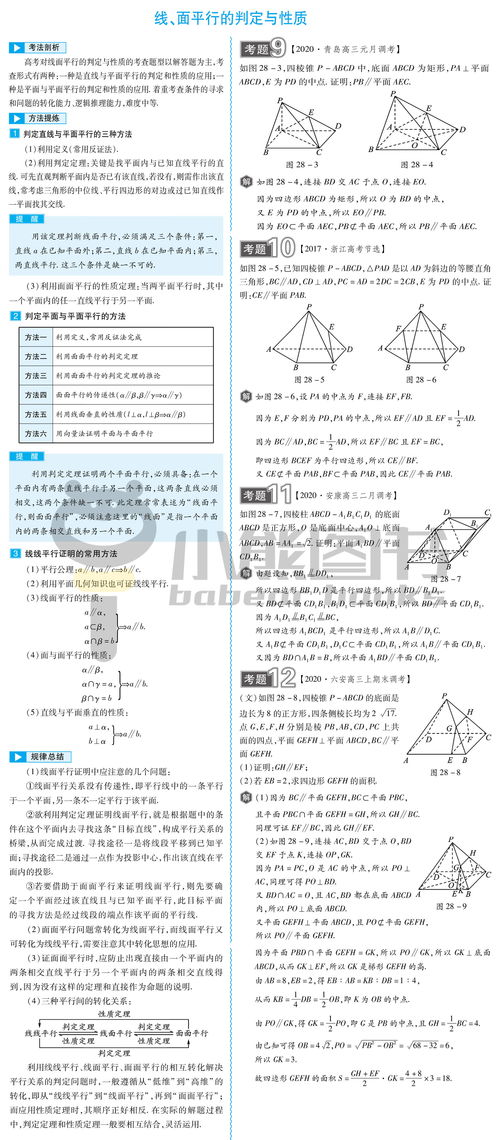
面面垂直的判定,面面垂直的判定

1、面面垂直的判定
面面垂直的判定定理:一個平面過另一平面的垂線,則這兩個平面相互垂直。如果一個平面的垂線平行于另一個平面,那么這兩個平面互相垂直。如果兩個平面的垂線互相垂直,那么這兩個平面互相垂直。
面面垂直的判定定理
1、在一個平面內做2條相交直線,另一個平面內有一條直線垂直于這兩條相交直線,則面面垂直。
2、如果兩個平面互相垂直,那么在一個平面內垂直于它們交線的直線垂直于另一個平面,則面面垂直。
3、如果一個平面經過另一平面的垂線,則這兩個平面相互垂直。
面面垂直的證明方法
1、定義法:如果兩個平面所成的二面角為90°,那么這兩個平面垂直。
2、判定定理:如果一個平面經過另一個平面的一條垂線,那么這兩個平面互相垂直。
3、如果一個平面內任意點在另外一個平面的射影均在這兩個平面的交線上,那么垂直。
4、如果N個互相平行的平面有一個垂直于一個平面,那么其余平面均垂直這個平面。
2、面面垂直的判定定理是什么?
共三個定理:
1、在一個平面內做2條相交直線,另一個zhi平面內有一條直線垂直于這兩條相交直線,則面面垂直。
2、如果兩個平面互相垂直,那么在一個平面內垂直于它們交線的直線垂直于另一個平面。 面面垂直。
3、如果一個平面經過另一平面的垂線,則這兩個平面相互垂直。
一個平面過另一平面的垂線,則這兩個平面相互垂直。
幾何描述:若a⊥β,a?α,則α⊥β
證明:任意兩個平面關系為相交或平行,設a⊥β,垂足為P,那么P∈β
∵a?α,P∈a
∴P∈α
即α和β有公共點P,因此α與β相交。
設α∩β=b,∵P是α和β的公共點
∴P∈b
過P在β內作c⊥b
∵b?β,a⊥β
∴a⊥b,垂足為P
又c⊥b,垂足為P
∴∠aPc是二面角α-b-β的平面角
∵c?β
∴a⊥c,即∠aPc=90°
根據面面垂直的定義,α⊥β
3、面面垂直的判定定理是什么
4、面面垂直的條件是什么
1.如果兩個平面相互垂直,那么在一個平面內垂直于它們交線的直線垂直于另一個平面。
2.如果兩個平面相互垂直,那么經過第一個平面內的一點作垂直于第二個平面的直線在第一個平面內。
3.如果兩個相交平面都垂直于第三個平面,那么它們的交線垂直于第三個平面。
4.如果兩個平面互相垂直,那么一個平面的垂線與另一個平面平行。
直線與平面垂直的判定定理(線面垂直定理):一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直。
推論1:如果在兩條平行直線中,有一條直線垂直于一個平面,那么另一條直線也垂直于這個平面。
推論2:如果兩條直線垂直于同一個平面,那么這兩條直線平行。
"/>

請添加微信號咨詢:19071507959
最新更新
推薦閱讀
猜你喜歡
關注我們


 留學規劃
留學規劃  留學考試
留學考試  留學指南
留學指南  留學攻略
留學攻略  留學生活
留學生活  留學信息
留學信息  留學專業
留學專業  留學簽證
留學簽證  關于我們
關于我們  網站首頁
網站首頁








